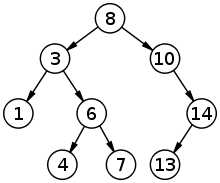
"이진 검색 트리"(Binray Search Tree)는 다음과 같은 성질을 만족하는 이진트리이다.
- 각 노드에 들어가는 값들은 대소관계를 비교할 수 있다.
- 노드의 왼쪽 서브트리는 작은 값들을 가진 노드들로 이루어져 있다.
- 노드의 오른쪽 서브트리는 큰 값들을 가진 노드들로 이루어져 있다.
- 좌우 서브트리는 각각 위의 2 조건을 만족한다.

이러한 특성 때문에 정렬된 이진 트리(Sorted Binary Tree)라고도 부른다.
이진 검색 트리는 검색, 삽입, 삭제 연산들이 평균적으로 $O(logN)$에 동작한다.
해시의 경우, 위의 연산들을 $O(1)$에 제공하지만, 원소 간의 대소관계는 비교할 수 없다.
하지만, 이진 검색 트리의 경우 "5 보다 큰 최초의 원소"와 같은 대소비교 관련 연산을 수행할 수 있다.
힙 자료구조의 경우 가장 크거나 가장 작은 하나의 원소만 알 수 있지 대소관계는 알 수 없다.
기능
검색
검색은 루트노드부터 시작해 다음과 같은 과정을 수행한다.
- 검색 값과 현재 값을 비교해, 크다면 오른쪽으로 작다면, 왼쪽으로 이동한다.
- 이를 원하는 값을 찾을때까지 재귀적으로 반복한다.
39를 찾는 과정을 예시로 살펴보자.

다음과 같이 탐색의 시간 복잡도의 경우는 트리의 높이에 비례하기 때문에 평균적으로 $O(logN)$이 소요된다.
삽입
이진 검색 트리는 중복을 허용하지 않는다.
이러한 이진 검색 트리에서 삽입은 다음과 같이 동작한다.
- 우선, 삽입을 수행하기 전에 검색을 수행한다.
- 검색을 통해, 리프노드에 도달하면 해당 노드와 키 값을 비교해 삽입할 위치를 결정한다.
다음 예시는 37인 노드를 삽입하는 과정이다.

삭제
이진 검색 트리의 삭제의 경우는 3가지 상황으로 구분된다.
- 리프노드를 삭제하는 경우
- 자식 노드가 1개인 노드를 삭제하는 경우
- 자식 노드가 2개인 노드를 삭제하는 경우
리프노드를 삭제하는 경우
리프 노드는 탐색을 거친 후, 해당 위치의 원소를 삭제하면 된다.

자식 노드가 1개인 노드를 삭제하는 경우
자식이 한개인 노드를 삭제하는 경우는 해당 노드를 삭제하고, 그 위치에 해당 노드의 자식노드를 대입한다.

자식 노드가 2개인 노드를 삭제하는 경우
자식 노드가 2개인 경우에는 2가지 방법이 존재한다.
- 왼쪽 서브트리에서 가장 큰 값으로 대체
- 오른쪽 서브트리에서 가장 작은 값으로 대체
이때, 대체하는 노드를 successor라 부른다.

이진 탐색 트리의 문제점
이진 탐색 트리에서 모든 연산은 트리의 높이에 비례한다.
평균의 경우 $O(logN)$이지만, 아래와 같이 편향트리가 되는 경우 시간복잡도는 $O(N)$이다.

따라서, 시작복잡도가 $O(logN)$가 되도록 균형트리를 보장하는 트리인 AVL 혹은 Red-Black을 사용한다.
구현
전체적인 구현은 여기에서 확인해 볼 수 있다.
https://github.com/jungseokyoung-cloud/Data-Structure/tree/main/Data-Structure/Tree.playground
Data-Structure/Data-Structure/Tree.playground at main · jungseokyoung-cloud/Data-Structure
Data Structures implemented with Swift. Contribute to jungseokyoung-cloud/Data-Structure development by creating an account on GitHub.
github.com
우선, 노드부터 정의해 보자.
Node
final class Node<T: Comparable> {
var value: T
var left: Node?
var right: Node?
var height: Int
weak var parent: Node?
init(value: T, height: Int = 0) {
self.value = value
self.height = height
}
init(value: T, parent: Node<T>?, height: Int = 0) {
self.value = value
self.parent = parent
self.height = height
}
}
// MARK: - Extension
extension Node {
var balanceFactor: Int {
return (self.right?.height ?? 0) - (self.left?.height ?? 0)
}
var isRoot: Bool {
parent == nil
}
var isLeaf: Bool {
self.right == nil && self.left == nil
}
var isLeftChild: Bool {
parent?.left === self
}
var isRightChild: Bool {
parent?.right === self
}
var hasLeftChild: Bool {
self.left != nil
}
}Node는 다음과 같이 정의했으며, 이진 검색 트리에서 값들은 대소관계 비교할 수 있어야 하기 때문에 값들은 Comparable프로토콜을 만족하는 제네릭으로 제한했다.
또한, left와 right 자식들의 경우는 강한 참조로 들고 있지만, 순환참조 우려에 의해 parent는 약한 참조로 참조했다.
다음으로 트리는 다음과 같다.
public class BinarySearchTree<T: Comparable> {
/// 트리의 루트노드입니다.
private(set) var root: Node<T>?
public var isEmpty: Bool { size == 0 }
public private(set) var size: Int = 0
public init() { }
}
insert(_:)
// MARK: - Insert Method
/// tree에 값을 추가합니다.
public func insert(_ value: T) {
guard let root else {
self.root = Node(value: value)
return
}
// 이미 값이 존재하는 경우
guard !contain(value) else { return }
var current = root
size += 1
while true {
if current.value > value {
if let next = current.left {
current = next
} else {
current.left = Node(value: value, parent: current)
return
}
} else {
if let next = current.right {
current = next
} else {
current.right = Node(value: value, parent: current)
return
}
}
}
}insert(_:) 메서드는 BST에 규칙에 맞게 값을 추가한다.
다음과 같이 수행한다.
- 비어있는 경우라면, root를 새로운 노드로 지정한다.
- 루프노드부터 시작해 추가할 값이 더 크다면 오른쪽 자식으로, 더 작다면 왼쪽 자식으로 이동한다.
- 이 과정을 리프노드가 될 때까지 반복한다.
- 리프노드에 대소 비교를 통해 오른쪽 자식 혹은 왼쪽 자식으로 추가한다.
contain(_:)
private func search(_ value: T) -> Node<T>? {
guard root != nil else { return nil }
var current = root
while let node = current {
if node.value == value { return node }
if node.value > value {
current = node.left
} else {
current = node.right
}
}
return nil
}contain(_:) 메서드를 살펴보기 전에 search(_:)메서드부터 살펴보면, value에 맞는 node를 반환하는 함수이다.
public func contain(_ value: T) -> Bool {
return search(value) != nil
}이후, contain(_:) 메서드는 다음과 같이 해당 값이 존재하는지 여부를 리턴한다.
remove(_:)
remove의 경우에는 앞서 말했듯 총 3 자기 경우의 수로 나뉜다.
- 리프 노드를 삭제하는 경우
- 자식이 한개인 노드를 삭제하는 경우
- 자식이 두개인 노드를 삭제하는 경우
// MARK: - Remove Method
public func remove(_ value: T) -> T? {
guard let node = search(value) else { return nil }
defer { size -= 1 }
// 리프 노드인 경우
if node.isLeaf {
return removeLeafNode(node)
// 왼쪽 자식만 존재하는 경우
} else if let leftNode = node.left, node.right == nil {
return removeOneChildNode(node, child: leftNode)
// 오른쪽 자식만 존재하는 경우
} else if let rightNode = node.right, node.left == nil {
return removeOneChildNode(node, child: rightNode)
// 자식이 두개인 노드인 경우
} else {
guard let rightNode = node.right else { return nil }
let successor = successor(from: rightNode)
return removeTwoChildNode(node, successor: successor)
}
}
리프 노드를 삭제하는 경우
// 리프 노드인 경우
if node.isLeaf {
return removeLeafNode(node)
}
func removeLeafNode(_ node: Node<T>) -> T? {
defer {
if node.isLeftChild {
node.parent?.left = nil
} else {
node.parent?.right = nil
}
if node === root { root = nil }
}
return node.value
}우선, 삭제할 노드가 parent의 left 자식인 경우 parent.left = nil로 right 자식인 경우, parent.right = nil로 세팅한다.
이로써, 기존 노드를 reference count가 감소해 메모리에서 해제될 수 있다.
만약, root노드인 경우라면, root = nil로 설정해 완전히 메모리에서 해제될 수 있게 한다.
자식이 한개인 노드를 삭제하는 경우
// 왼쪽 자식만 존재하는 경우
else if let leftNode = node.left, node.right == nil {
return removeOneChildNode(node, child: leftNode)
// 오른쪽 자식만 존재하는 경우
} else if let rightNode = node.right, node.left == nil {
return removeOneChildNode(node, child: rightNode)
func removeOneChildNode(_ node: Node<T>, child: Node<T>) -> T? {
defer {
if node.isLeftChild {
node.parent?.left = child
} else {
node.parent?.right = child
}
child.parent = node.parent
if node === root { root = child }
}
return node.value
}우선, node의 위치를 child로 대체한다.
이후, child의 parent를 갱신해 준다.
자식이 두개인 노드를 삭제하는 경우
// 자식이 두개인 노드인 경우
else {
guard let rightNode = node.right else { return nil }
let successor = successor(from: rightNode)
return removeTwoChildNode(node, successor: successor)
}
우선, 대체할 노드 successor는 오른쪽 서브트리의 최솟값으로 구현했다.
private func successor(from node: Node<T>) -> Node<T> {
var current = node
while let leftNode = current.left { current = leftNode }
return current
}
다음으로 이 successor를 삭제할 노드로 대체한다.
func removeTwoChildNode(_ node: Node<T>, successor: Node<T>) -> T? {
if node.isLeftChild {
node.parent?.left = successor
} else {
node.parent?.right = successor
}
if successor.isLeftChild {
successor.parent?.left = successor.right
successor.right?.parent = successor.parent
} else {
successor.parent?.right = successor.right
successor.right?.parent = successor.parent
}
successor.parent = node.parent
successor.left = node.left
successor.right = node.right
successor.left?.parent = successor
successor.right?.parent = successor
if node === root { root = successor }
return node.value
}해당 경우에는 2가지 경우의 수로 나뉜다.
- successor가 리프노드인 경우
- successor가 오른쪽 자식이 존재하는 경우
우선, successor는 오른쪽 서브트리에 가장 작은 값으로 했기 때문에, 왼쪽 자식이 없는 것은 자명하다.
만약, successor가 리프 노드인 경우는 다음과 같이 단순히 삭제할 노드와 대체하면 된다.

하지만, 오른쪽 자식이 존재하는 경우, 다음과 같이 successor자리로 오른쪽 자식을 이동하는 작업이 필요하다.

이제 코드를 살펴보면 다음과 같다.
// 기존 node의 parent의 자식을 successor로 지정한다.
if node.isLeftChild {
node.parent?.left = successor
} else {
node.parent?.right = successor
}
// successor의 오른쪽에 있는 자식을 자신의 자리로 이동시킨다.
// successor는 오른쪽 서브트리에 가장 왼쪽에 위치하기에 left자식
if successor.isLeftChild {
successor.parent?.left = successor.right
successor.right?.parent = successor.parent
} else {
successor.parent?.right = successor.right
successor.right?.parent = successor.parent
}
// node의 위치에 successor 주입
successor.parent = node.parent
successor.left = node.left
successor.right = node.right
// 기존 node의 자식이었던 노드들의 부모를 successor로 변경
successor.left?.parent = successor
successor.right?.parent = successor
if node === root { root = successor }
References
위키 백과
https://www.kodeco.com/990-swift-algorithm-club-swift-binary-search-tree-data-structure
'CS > Data Structure' 카테고리의 다른 글
| [Data Structure] Tree(4) - Red-Black Tree (1) | 2024.06.02 |
|---|---|
| [Data Structure] Tree(3) - AVL Tree (0) | 2024.05.23 |
| [Data Structure] Tree(1) (0) | 2024.05.12 |
| [Data Structure] Graph (1) | 2024.05.06 |
| [Data Structure] Hash Table(2) - Implementation (0) | 2024.04.29 |