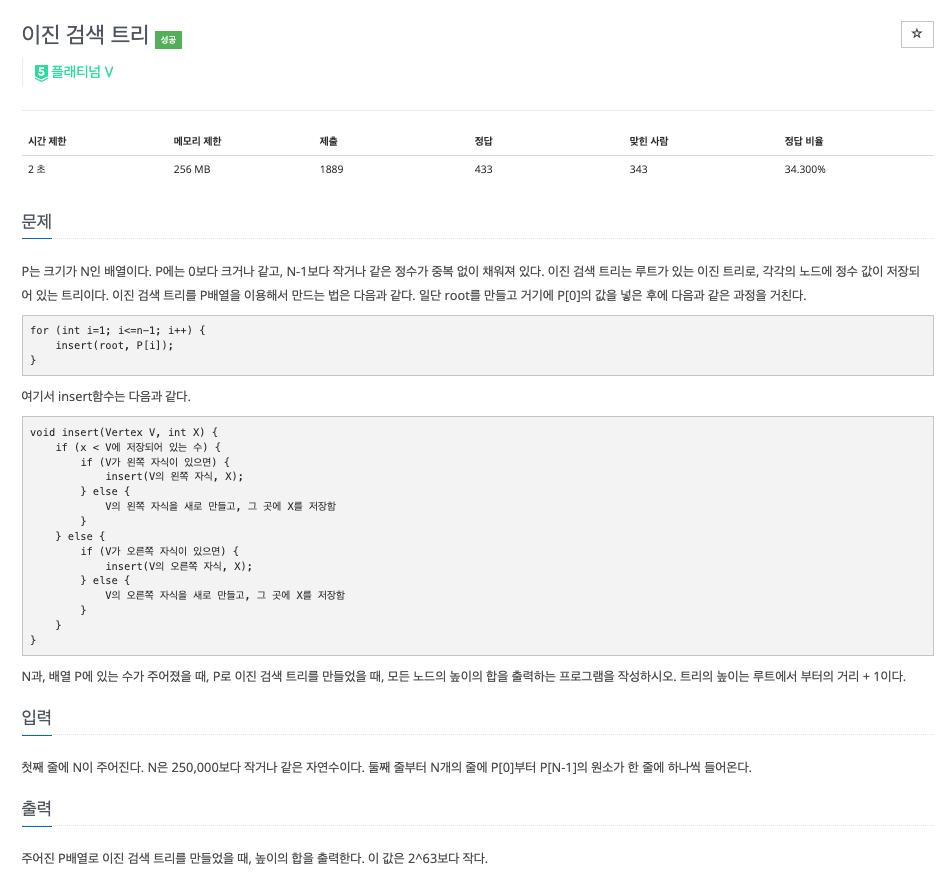

https://www.acmicpc.net/problem/1539
문제 접근
가장 먼저 생각할 수 있는 방법은 BST를 직접 구현해, 삽입될 때마다 위치를 확인하는 방법이다.
하지만, N = 250,000이고, BST가 편향 트리가 되는 경우 탐색 시간은 $O(logN)$이 아닌, $O(N)$이 되게 되어,
최종 시간 복잡도는 $O(N^2)$으로 시간초과가 발생하게 된다.
그렇다면, Self-Balancing 트리를 사용하면서 BST상에서 노드의 높이를 알 수 있어야만 한다.
이때, 노드가 삽입될 때, 부모 노드의 높이를 알 수만 있다면, 각 노드의 높이를 계산할 수 있을 것이다.
따라서, Self-Balancing 트리에서 새로운 노드가 삽입되는 부모 노드를 알아야 한다.
트리에서 새로운 노드는 "자신보다 바로 작거나 큰 값을 가진 노드"의 자식으로 삽입될 것이다.
우선, "자신보다 바로 큰 값을 가진 노드"의 자식으로 삽입되는 상황을 살펴보자.
해당 경우에는 왼쪽 자식으로 삽입되게 될 것이다.
하지만, 왼쪽 자식이 있는 경우라면, "자신보다 바로 작은 값을 가진 노드"의 자식으로 삽입되어야 한다.
해당 경우에는 오른쪽 자식으로 삽입되게 될 것이다.
그렇다면, 오른쪽 자식이 있는 경우라면 어떻게 될까?
결론부터 말하자면, "자신보다 바로 큰 값을 가진 노드"부터 확인한다면, 해당 경우는 존재하지 않는다.
만약, 삽입되는 노드를 X라고 가정하고, 부모 노드를 Y라고 가정하자.
노드 X와 노드 Y의 값들을 각각 $x$, $y$라고 가정한다면,
"자신보다 바로 작은 값을 가진 노드"의 자식으로 삽입되었기 때문에, 항상 $y < x$를 만족한다.
이때, Y의 오른쪽 자식을 K라고 가정해 보고, 값을 $k$라고 가정해 보자.
그렇다면 $y < k$가 되며, 노드 K는 "X보다 바로 큰 값을 가진 노드"가 된다.
노드 Y가 "X보다 바로 작은 값을 가진 노드"이기 때문에, $y < k < x$는 성립할 수 없다.
하지만, 해당 케이스는 우선적으로 "자신보다 바로 큰 값을 가진 노드"부터 확인한 경우라면,
Y의 오른쪽 자식이 존재할 수 있는 경우는 없다.
문제 풀이
즉, 이를 코드로 옮겨보자면 다음과 같다.
우선, lower_bound를 통해 "자신보다 바로 큰 값을 가진 노드"를 확인한다.
하지만, 자신보다 바로 큰 값이 없는 경우, 해당 경우는 삽입되는 노드가 가장 큰 값이다.
따라서, "자신보다 바로 작은 값을 가진 노드"의 오른쪽 자식으로 삽입한다.
auto iter = node.lower_bound(num);
if(iter == node.end()) {
advance(iter, -1);
iter->second.hasRight = true;
node[num] = {false, false, iter->second.height + 1};
}
다음으로, "자신보다 바로 큰 값을 가진 노드"의 왼쪽 자식이 이미 존재하는 경우에는 "자신보다 바로 작은 값을 가진 노드"의 오른쪽 자식으로 삽입한다.
반대의 경우 왼쪽 자식으로 그대로 삽입하면 된다.
else {
// 왼쪽이 있는 경우
if(iter->second.hasLeft) {
advance(iter, -1);
iter->second.hasRight = true;
node[num] = {false, false, iter->second.height + 1};
// 왼쪽이 없는 경우
} else {
iter->second.hasLeft = true;
node[num] = {false, false, iter->second.height + 1};
}
}
전체 코드
#include <iostream>
#include <map>
using namespace std;
#define FAST ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define endl '\n'
#define ll long long
struct NodeInfo {
bool hasLeft, hasRight;
int height;
};
int N;
map<int, NodeInfo> node;
ll solve() {
ll total = 0;
cin >> N;
int num;
for(int i = 0; i < N; i++) {
cin >> num;
if(node.size() == 0) {
node[num] = {false, false, 1};
continue;
}
auto iter = node.lower_bound(num);
if(iter == node.end()) {
advance(iter, -1);
iter->second.hasRight = true;
node[num] = {false, false, iter->second.height + 1};
} else {
// 왼쪽이 있는 경우
if(iter->second.hasLeft) {
advance(iter, -1);
iter->second.hasRight = true;
node[num] = {false, false, iter->second.height + 1};
// 왼쪽이 없는 경우
} else {
iter->second.hasLeft = true;
node[num] = {false, false, iter->second.height + 1};
}
}
}
for(auto res: node) {
total += res.second.height;
}
return total;
}
int main(){
FAST;
cout << solve() << endl;
}'CS > Algorithm' 카테고리의 다른 글
| [Algorithm] 정렬 알고리즘(2) - 머지 소트, 퀵 소트, 기수 정렬 (0) | 2024.08.12 |
|---|---|
| [Algorithm] 정렬 알고리즘(1) - 버블정렬, 선택정렬, 삽입정렬 (0) | 2024.07.10 |
| [Algorithm] 알고리즘이란? (1) | 2024.07.08 |
| [PS] BOJ 2457 (공주님의 정원) (0) | 2024.06.23 |
| [PS] BOJ 1019(책 페이지) - C++ (0) | 2024.04.06 |